Research
Our research aims to develop novel ways of computing, circuit design, and reliability for electronic circuits and systems. Our research mainly targets emerging technologies and new computing paradigms.
Contents |
Computing with Nano-Crossbar Arrays | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nano-crossbar arrays have emerged as a strong candidate technology to replace CMOS in near future. They are regular and dense structures, and fabricated by exploiting self-assembly as opposed to purely using lithography based conventional and relatively costly CMOS fabrication techniques. Currently, nano-crossbar arrays are fabricated such that each crosspoint can be used as a conventional electronic component such as a diode, a FET, or a switch. This is a unique opportunity that allows us to integrate well developed conventional circuit design techniques into nano-crossbar arrays. Motivated by this, we aim to develop a complete synthesis and performance optimization methodology for switching nano-crossbar arrays that leads to the design and construction of an emerging nanocomputer.
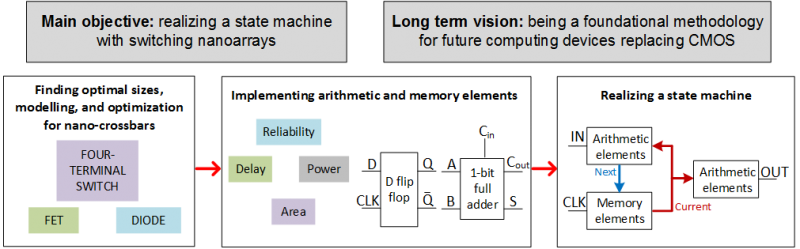 SynthesisWe study implementation of Boolean functions with nano-crossbar arrays where each crosspoint behaves as a diode, a FET, and a four-terminal switch. For these three types, we give array size formulations for a given Boolean function. Additionally, we focus on four-terminal switch based implementations and propose an algorithm that implements Boolean functions with optimal array sizes. Fault ToleranceWe examine reconfigurable crossbar arrays by considering randomly occurred stuck-open and stuck-closed crosspoint faults. In the presence of permanent faults, a fast and accurate heuristic algorithm is proposed that uses the techniques of index sorting, backtracking, and row matching. In the presence of transient faults, tolerance analysis is performed by formally and recursively determining tolerable fault positions.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reversible Circuit Design | ||||||||||||||||||||||||||||||||||
|
Unlike conventional logic gates, reversible logic gates do not have “don’t-care” conditions. It means that an error occurring in any node of a reversible circuit is always seen at the output that gives a unique opportunity for error detecting/correcting. Motivated by this, we implement error tolerant reversible circuit blocks by exploiting parity preserving logic and Hamming codes. We aim to design, fabricate, and test a fault-aware 8-bit reversible microprocessor for applications requiring high accuracy and reliability including aerospace, military, and medical applications. 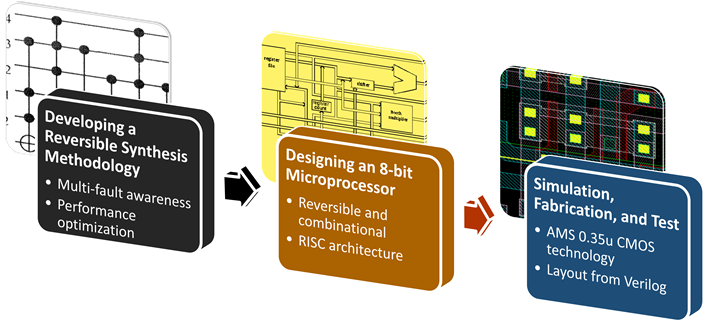 Synthesis and OptimizationWe propose a fast synthesis algorithm that implements any given reversible Boolean function with quantum gates. Instead of an exhaustive search on every given function, our algorithm creates a library of essential functions and performs sorting. As an example, to implement 4 bit circuits we only use 120 essential functions out of all 20922789888000 functions. We also perform optimization for both reversible and quantum circuit costs by considering adjacent gate pairs.
| ||||||||||||||||||||||||||||||||||
Stochastic Circuit Design | |||||||||||||||||||||||||
Accurate Arithmetic ImplementationsWe propose a method to overcome the main drawback in stochastic computing, low accuracy or related long computing times. Our method manipulates stochastic bit streams with the aid of feedback mechanisms. We implement error-free arithmetic multiplier and adder circuits by considering performance parameters area, delay, and accuracy. 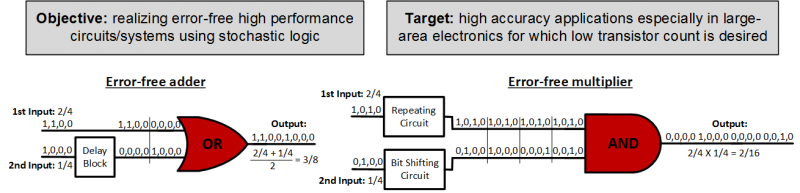
| |||||||||||||||||||||||||
Reliability of Electronic Products | |
|
The rapid developments in electronics, especially in the last decade, have elevated the importance of electronics reliability. Conventionally used accelerated reliability tests have lost their significance; time consuming and expensive feature of these tests is against the demands of today's very rapid electronic product cycles. In this study, we propose less costly, yet accurate, reliability prediction techniques using field return data, new accelerated test methodologies, and physics of failure based simulations. We cooperate with one of the Europe’s largest household appliance companies Arçelik A.Ş.. 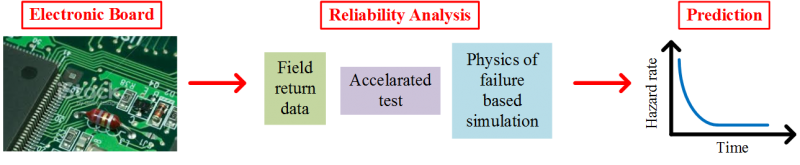 Reliability Analysis and Prediction with Field DataWe propose an accurate reliability prediction model for high-volume electronic products throughout their warranty periods by using field return data. Our model is constructed on a Weibull-exponential hazard rate scheme by using the proposed change point detection method based on backward and forward data analysis. Our prediction model can make a 36-month (full warranty) reliability prediction of an electronic board with using its field data as short as 3 months. Degradation Processes in VaristorsWe investigate different degradation mechanisms of ZnO varistors. We propose a model showing how the varistor voltage Vv changes by time for different stress levels. For this purpose, accelerated degradation tests are applied for different AC current levels; then voltage values are measured. Different from the common practice in the literature that considers a degradation with only decreasing Vv values, we demonstrate either an increasing or a decreasing trend in the Vv parameter. Calibrated Accelerated Life TestingDramatic decrease in failure rates for electronic products makes conventional accelerated life tests (ALT) extremely time consuming and costly. Recently proposed calibrated accelerated life tests (CALT) aim to use fewer samples than those used in ALT. We thoroughly compare ALT and CALT by considering the effects of failure rate, acceleration factor, and stress level on the required test time. | |
Analog Circuit Design | |||||||||||||||
Positive FeedbackThe conventional wisdom is that analog circuits should not include positive feedback loops. As controversial as it seems, we have successfully used positive feedback for impedance improvement in a current amplifier. With adding few transistors we have achieved very low input resistance values. Additionally, we have proposed a new fully-differential current amplifier and tested it in a filter application.
| |||||||||||||||
Discrete Mathematics | |||||||||||||
Self Duality ProblemThe problem of testing whether a monotone Boolean function in irredundant disjuntive normal form (IDNF) is self-dual is one of few problems in circuit/time complexity whose precise tractability status is unknown. We have focused on this famous problem. We have shown that monotone self-dual Boolean functions in IDNF do not have more variables than disjuncts. We have proposed an algorithm to test whether a monotone Boolean function in IDNF with n variables and n disjuncts is self-dual. The algorithm runs in O(n^3) time.
| |||||||||||||

