Araştırma
| Line 861: | Line 861: | ||
|} | |} | ||
|} | |} | ||
| − | {| style="margin-left: auto; margin-right: 0px; border:1px solid #abd5f5; background:#f1f5fc;" | + | <!-- {| style="margin-left: auto; margin-right: 0px; border:1px solid #abd5f5; background:#f1f5fc;" |
| | | | ||
| Line 876: | Line 876: | ||
|} | |} | ||
| − | |} | + | |} --> |
|} | |} | ||
Revision as of 16:31, 20 April 2019
Araştırmalarımızın amacı, elektronik devre ve sistemler için hesaplama, devre tasarımı ve güvenilirlik konularında yeni yaklaşımlar geliştirmektir. Araştırmalarımız temelde yeni ve gelişen teknolojileri ve hesaplama düzenlerini hedef almaktadır. Aşağıda en yeniden en eskiye ve önem sırasına göre sıralanan araştırma konuları yer almaktadır. Her konu kısaca anlatılmış ve ilgili yayın ve projeler eklenmiştir.
Contents |
Nano-Çaprazlayıcı Dizinler ile Hesaplama | ||||||||||||||||||||||||||||||||||||||
|
Nano-çaprazlayıcı dizinler yakın gelecekte CMOS'un yerini alacak güçlü bir aday teknoloji olarak ortaya çıkmıştır. Düzenli ve sık yapıdadırlar. Dizinler ile hesaplama, iki-uçlu ya da dört-uçlu anahtarlar gibi davranan çaprazlama noktaları ile elde edilir. Kullanılan teknolojiye bağlı olarak, iki-uçlu bir anahtar, diyot, direnç/memristor veya FET gibi davranır. Öte yandan, dört-uçlu anahtarın tek bir davranışı vardır. İki-uçlu anahtar tabanlı dizinler için önerilen birçok farklı teknoloji olmasına rağmen, dört-uçlu anahtar tabanlı dizinler, anahtarlamalı kafesler, için teknoloji geliştirme yakın zamanda başlamıştır. Hem iki-uçlu hem de dört-uçlu anahtar tabanlı dizinler için, ortaya çıkacak bir nano bilgisayarın tasarımı ve yapımı için tam bir sentez ve performans optimizasyon metodolojisi geliştirmeyi hedefliyoruz. Ayrıca, özellikle anahtarlamalı kafesleri gerçeklemek için CMOS uyumlu teknolojiler geliştirmeyi hedefliyoruz. 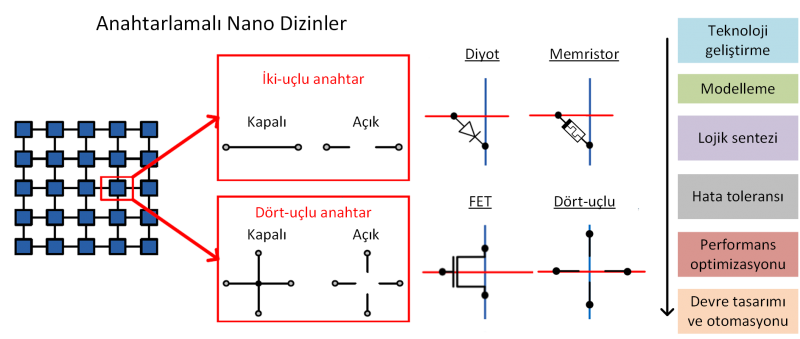 Teknoloji GeliştirmeDört-uçlu anahtar tabanlı bir dizin, iki-uçlu anahtarlara kıyasla, anahtar sayısı bakımından önemli bir alan avantajı sunsa da, teknoloji seviyesinde gerçekleştirilmesi henüz net olarak cevaplanmamıştır. Bu ihtiyacı karşılamak için ilk olarak, üç boyutlu teknoloji bilgisayar destekli tasarım (TCAD) simülasyonları kullanarak, dört-uçlu anahtarların doğrudan CMOS teknolojisi ile gerçeklenebileceğini gösterdik. Bu amaçla farklı yarı iletken malzemelerini farklı geometrik şekillerde denedik. Ardından, TCAD simülasyon verilerini standart CMOS akım-gerilim denklemlerine uyarlayarak, dört-uçlu bir anahtarın Spice modelini geliştirdik. Son olarak, Spice devre simülasyonlarını farklı ebatlardaki dört-uçlu anahtarlarda başarıyla uyguladık. 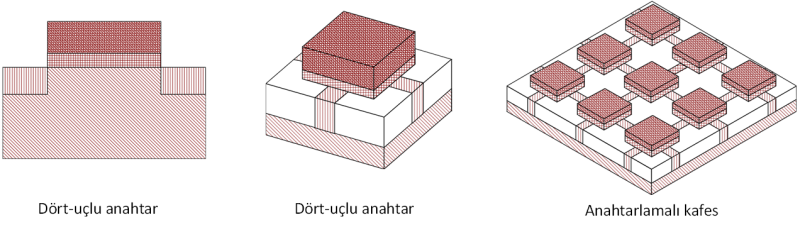 Performans OptimizasyonuMemristor tabanlı dizinleri de içeren nano anahtarlamalı dizinlerin optimizasyonu üzerine çalışıyoruz. Dizilerin alan, gecikme ve güç maliyetlerini dikkate alarak hataya dayanıklı lojik sentez algoritmaları önerdik. Hata ToleransıYeniden ayarlanabilir nano dizinlerde oluşan açık ve kapalı hataları inceledik. Kalıcı hatalar için, sıralama, geri-izleme ve satır eşleştirme tekniklerini kullanan hızlı bir buluşsal algoritma geliştirdik. Yumuşak/geçici hatalar için, tolere edilebilir bütün hata yerlerini yinelemeli bir teknik kullanarak belirledik. SentezBoolean fonksiyonları diyot, FET ve dört-uçlu anahtar tabanlı nano dizinler ile gerçekledik ve dizin boyut formülleri elde ettik. Buna ek olarak, dört-uçlu anahtarlardan oluşan dizinleri optimum sentezleyen bir algoritma geliştirdik.
| ||||||||||||||||||||||||||||||||||||||
Tersinir Hesaplama | |||||||||||||||||||||||||||||||||||
|
Geleneksel CMOS devrelerinden farklı olarak, tersinir devreler gizli hatalara sahip değildir, bu nedenle dahili devre düğümlerinde meydana gelen hatalar her zaman çıkışta bir hataya neden olur. Bu, çevrimiçi veya eşzamanlı hata toleransı için eşsiz bir özelliktir. Bu durumdan hareketle, tersinir hesaplamayı kullanarak hataya dayanıklı CMOS devre blokları gerçekliyoruz. Öncelikle tersinir kapılarla tersinir devreler sentezliyoruz; sonra onları hataya dayanıklı hale getiriyoruz; ve son olarak tersinir kapılardan CMOS kapılara dönüşümü yapıyoruz. 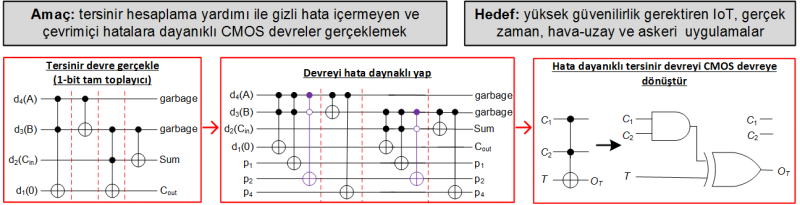 Mükemmel Hata TespitiTersinir hesaplamadan yararlanarak % 100 çevrimiçi veya eşzamanlı hata tespitine sahip CMOS devreleri sentezledik. Bu amaç için tersinir parite korunumlu bir kapı kütüphanesi önerdik. Çevrimiçi Hata Tespiti ve DüzeltmeÇoklu kontrol Toffoli kapılarını kullanarak tersine çevrilebilir bir devrede hataya dayanıklı hale getirmek için iki teknik geliştiriyoruz. İlk olarak, tek parite korumasına dayanan ve çıktıdaki tek sayıdaki hataları tespit edebilen bir teknik geliştirdik. İkinci teknik ise Hamming kodları üzerine inşa edilen bir hata düzeltme tekniğidir. Aynı zamanda, Fredkin kapısı gibi korunumlu tersinir kapılarla mükemmel hata tespitinin mümkün olduğunu gösterdik. Bir sonraki adım olarak, önerilen tersinir devreleri geleneksel CMOS kapılarından oluşan devrelere dönüştürdük.
| |||||||||||||||||||||||||||||||||||
Stokastik Devre Tasarımı | |||||||||||||||||||||||||||||
|
Rastgele veya Binom dağılımlı bit katarlarını işleyen yeni bir hesaplama paradigması “Bit Stream Computing (BSC)” önerdik. Önerilen paradigma, stokastik mantığın alan avantajından ve geleneksel ikili mantığın doğruluk avantajından faydalanmaktadır. Asenkron veya senkron olarak sınıflandırılmış tam ve yarı doğru aritmetik çarpıcı ve toplayıcı devreler gerçekledik. Bu çalışmanın, geleneksel ikili ve geleneksel stokastik hesaplama tekniklerine alternatif sunarak yeni ufuklar açtığına inanıyoruz. 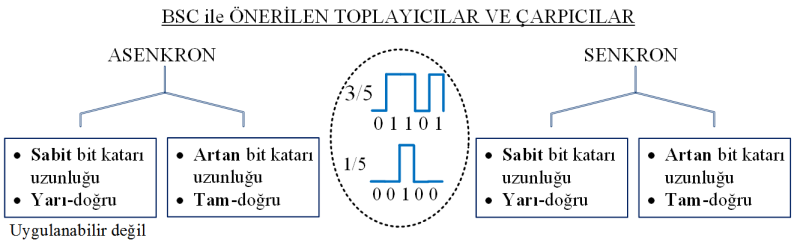
| |||||||||||||||||||||||||||||
Yaklaşık Devre ve Sistem Tasarımı | |||||||||||||||||||||||||||||
|
Bu çalışma, sistem düzeyinde tasarımın istenen doğrulukta olması için devre düzeyinde tasarımın güç/alan verimliliğini sağlar. İlk önce devre seviyesinde yaklaşık hesaplama blokları, genellikle toplayıcılar ve çarpıcılar, tasarladık. Daha sonra sistem seviyesinde, toplam hesaplama maliyetini en aza indiren ancak nihai performansı koruyan yaklaşık hesaplama birimlerini seçen bir yöntem geliştirildi. Yöntem, her bloğun yeterli çıktı kalitesini belirlemek için toplam sistemi en üst seviyeden aritmetik birimlerine kadar araştırmaktadır. 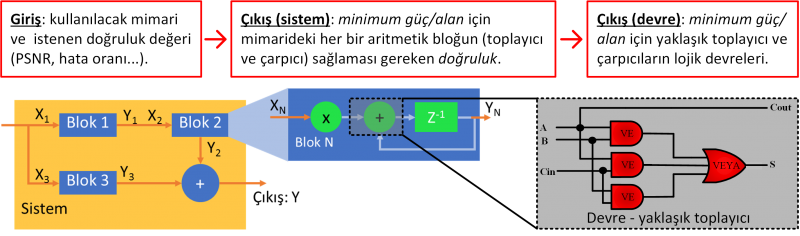
| |||||||||||||||||||||||||||||
Elektronik Ürünlerin Güvenilirliği | ||||||||||||||||||||||||||||||||||||||||
|
Elektronik sektöründe yaşanan baş döndürücü gelişmeler, elektronik devre ve sistemlerin güvenilirliği kavramını yeniden şekillendirmiştir. Elektronik ürünlerin günümüzdeki hızlı üretim döngüleri, uzun süreli ve masraflı olan geleneksel hızlandırılmış testlerin öneminin azalmasına neden olmuştur. Biz bu çalışmada görece masrafsız ve yüksek doğruluklu bir güvenilirlik analizi metodolojisi önerdik. Bu noktada saha verileri, yeni hızlandırılmış testler ve hata fiziği tabanlı benzetimlerden yararlandık. Çalışmalarımız Avrupa'nın en büyük ev aletleri ve beyaz eşya üreticilerinden biri olan Arçelik A.Ş. ile birlikte yürütülmüştür. 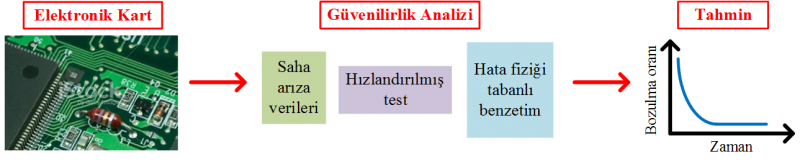 Saha Verileri ile Güvenilirlik Analizi ve TahminiYüksek miktarda üretilen elektronik ürünler için saha arıza verileri ile güvenilirlik tahmin modeli geliştirdik. Modelimizi, önerdiğimiz değişim noktası tespit metodunu kullanarak Weibul-eksponansiyel dağılımı üzerine inşa ettik. Modelimiz, elektronik kartların kısa süreli saha verilerini kullanarak, garanti süresi içerisindeki güvenilirlik performanslarını yüksek doğrulukta tahmin etmektedir. Bu çalışmada kullandığımız kartların garanti süresi 3 yıldır ve kullandığımız veri seti 3 aylıktır. Varistörlerin Bozunum ProsesleriZnO varistörlerde görülen değişik bozunum mekanizmalarını inceledik. Varistör voltajı Vv'nin değişik stres seviyelerinde nasıl değiştiğini modelledik. Bu amaç için, değişik AC akımlar kullanarak hızlandırılmış testler uyguladık ve Vv değerlerini ölçtük. Literatürdeki genel kanının aksine sadece düşen Vv değerleri değil, yükselen Vv değerleri de gözlemledik.
| ||||||||||||||||||||||||||||||||||||||||
Analog Devre Tasarımı | |||||||||||||||
Pozitif GeribeslemeGeleneksel olarak analog devreler pozitif geribesleme çevrimleri içermemelidirler. Aykırı gözükse de, biz bu çalışmada akım kuvvetlendiricilerin giriş empedanslarını pozitif geribesleme kullanarak başarıyla iyileştirdik. Ek olarak yeni bir tamamen farksal akım kuvvetlendirici devresi önerdik ve bu devreyi filtre uygulamalarında test ettik.
| |||||||||||||||
Ayrık Matematik | |||||||||||||
"Self Duality" ProblemiIDNF (irredundant disjuntive normal form) formundaki monoton bir Boolean fonksiyonun self-dual olup olmadığının zaman karmaşıklığında belirlenmesi, matematikte çözülememiş önemli problemlerden biridir. Bu çalışma bu ünlü problem üzerinedir. Biz bu çalışmada IDNF formundaki monoton Boolean fonksiyonların değişken sayısının çarpım (disjunct) sayısından fazla olamayacağını gösterdik. Ayrıca n sayıda çarpım ve n sayıda değişken içeren IDNF formundaki monoton Boolean fonksiyonların, self-dual olup olmadığını bulan bir algoritma geliştirdik. Algoritmanın zaman karmaşıklığı O(n^3)'dür.
| |||||||||||||

